6 多边形的面积
1 单元内容结构
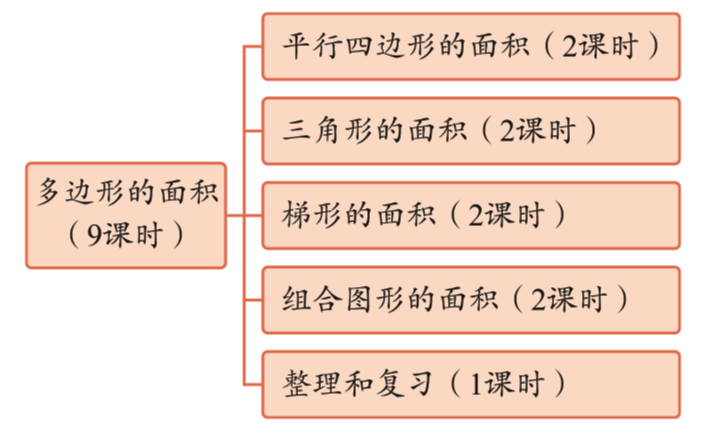
2 单元链接
| 年级 | 单元名 | 主要内容 |
|---|---|---|
| 三年级上册 | 7 长方形和正方形 | |
| 三年级下册 | 5 面积 | 基于对面积概念的理解,认识常见的面积单位,用数面积单位的方法探究长方形、正方形的面积公式,侧重面积含义的建立和长方形面积公式的推导。 |
| 四年级上册 | 5 平行四边形和梯形 | 基于对特殊四边形的研究,理解每个图形各自的特征,寻找关联,为后续面积的研究做铺垫,侧重图形边、角、高的研究。 |
| 四年级下册 | 5 三角形 | |
| 五年级上册 | 6 多边形的面积 | 基于长方形面积公式的推导过程,借助转化思想,帮助学生将未知图形的面积转化为已知图形的面积,侧重转化思想的运用。 |
| 五年级下册 | 3 长方体和正方体 | |
| 六年级上册 | 5 圆 | 基于对直边图形面积的研究,将转化的思想迁移到圆的面积的研究,侧重化曲为直、圆出于方的数学思想。 |
| 六年级下册 | 3 圆柱与圆锥 |
3 观点分享
3.1 以“度量”为核心目标
潘牡牡.梳结构找源头 突出概念本质——《多边形的面积》单元整合思考与实践[J].教学月刊小学版(数学),2020(12):21-24.
突出概念本质,面积的计算是面积单位的叠加。小学阶段度量教学内容及目标:
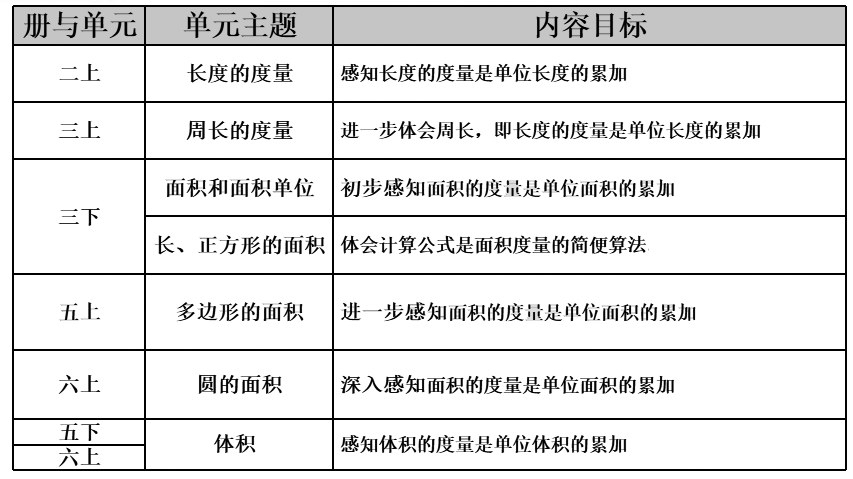
3.2 以方格纸为基本工具贯穿
刘克臣.以问题为驱动以问题为驱动,以工具为抓手,重构单元学习——“多边形的面积”教学研究[J].小学数学教师,2019(10):63-66.
面积单位和图形转化并重,螺旋上升贯穿面积度量的学习,在掌握方法(转化)的过程中理解知识本质(面积单位的个数累加),理法融合。
依据学生的疑问,以方格纸为基本工具贯穿本单元学习,具体框架如下。
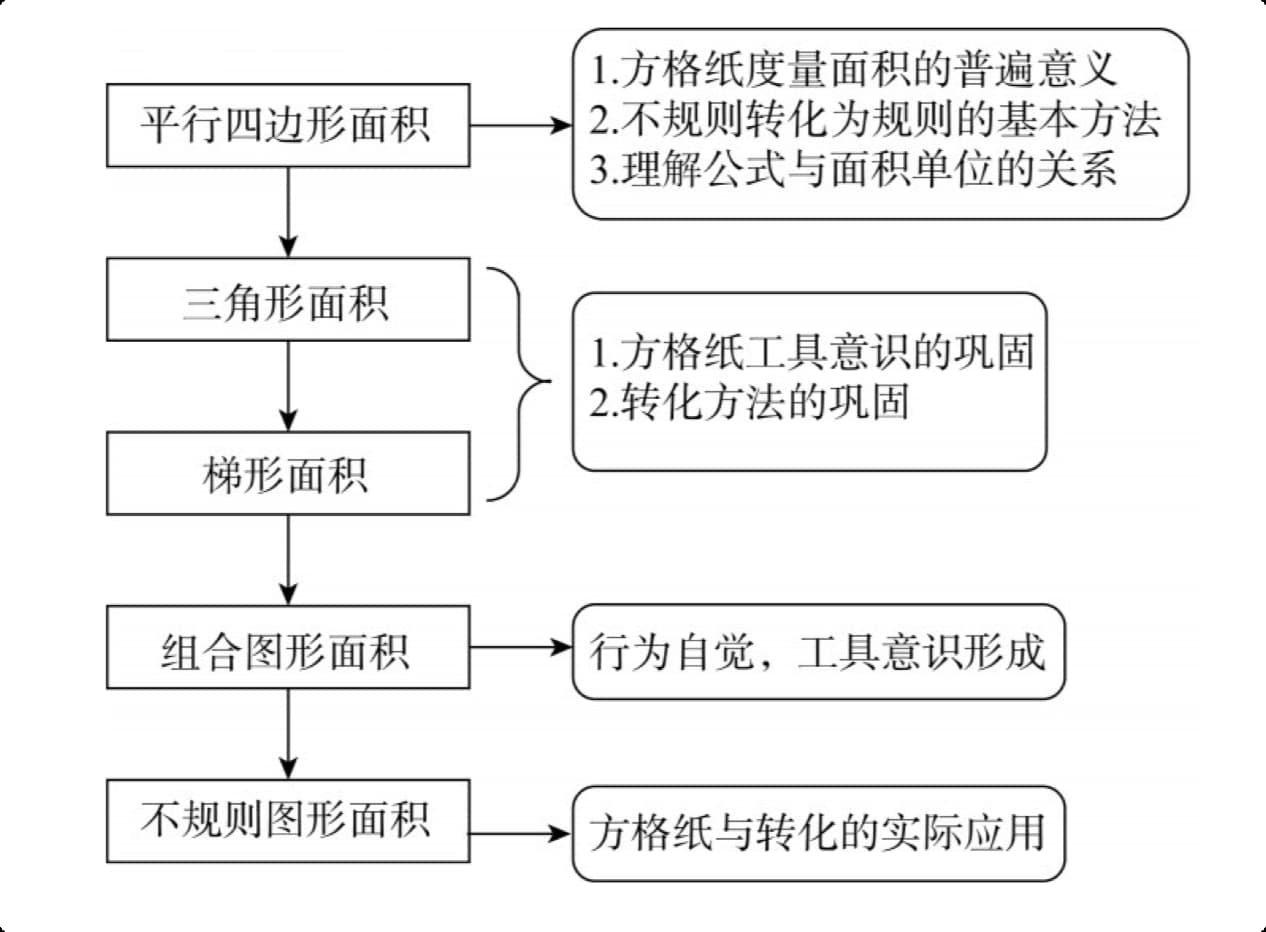
4 电子教材



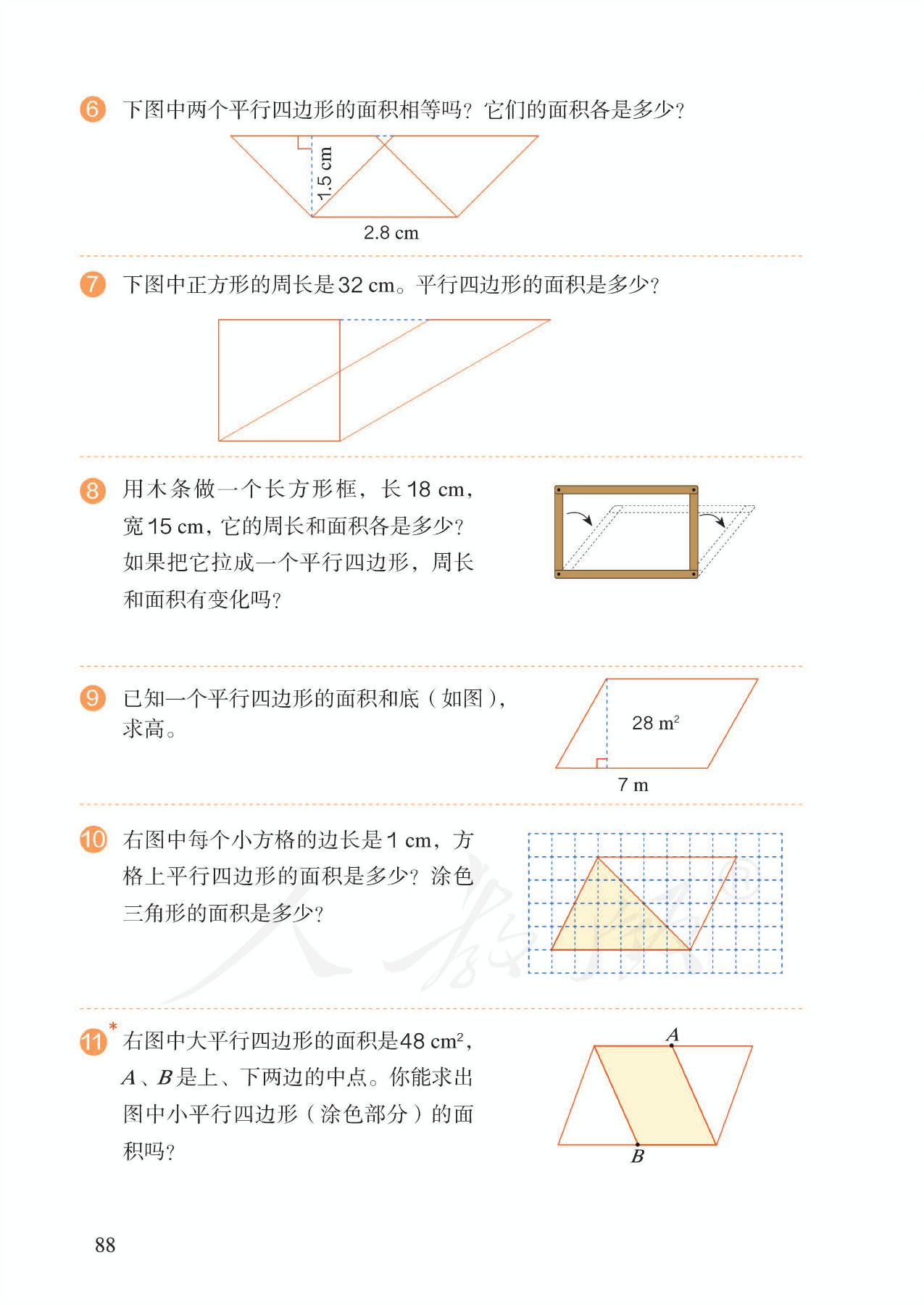
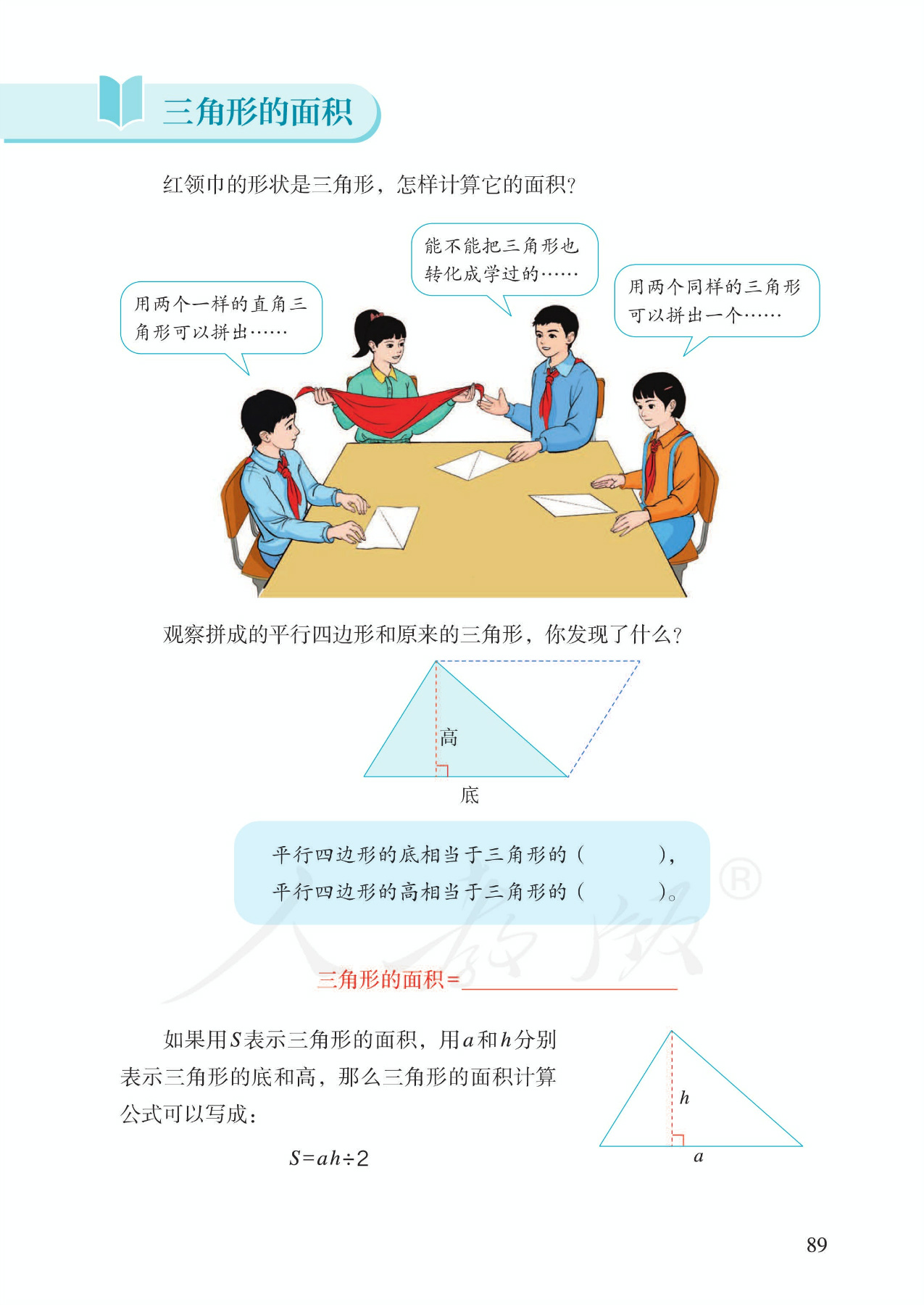
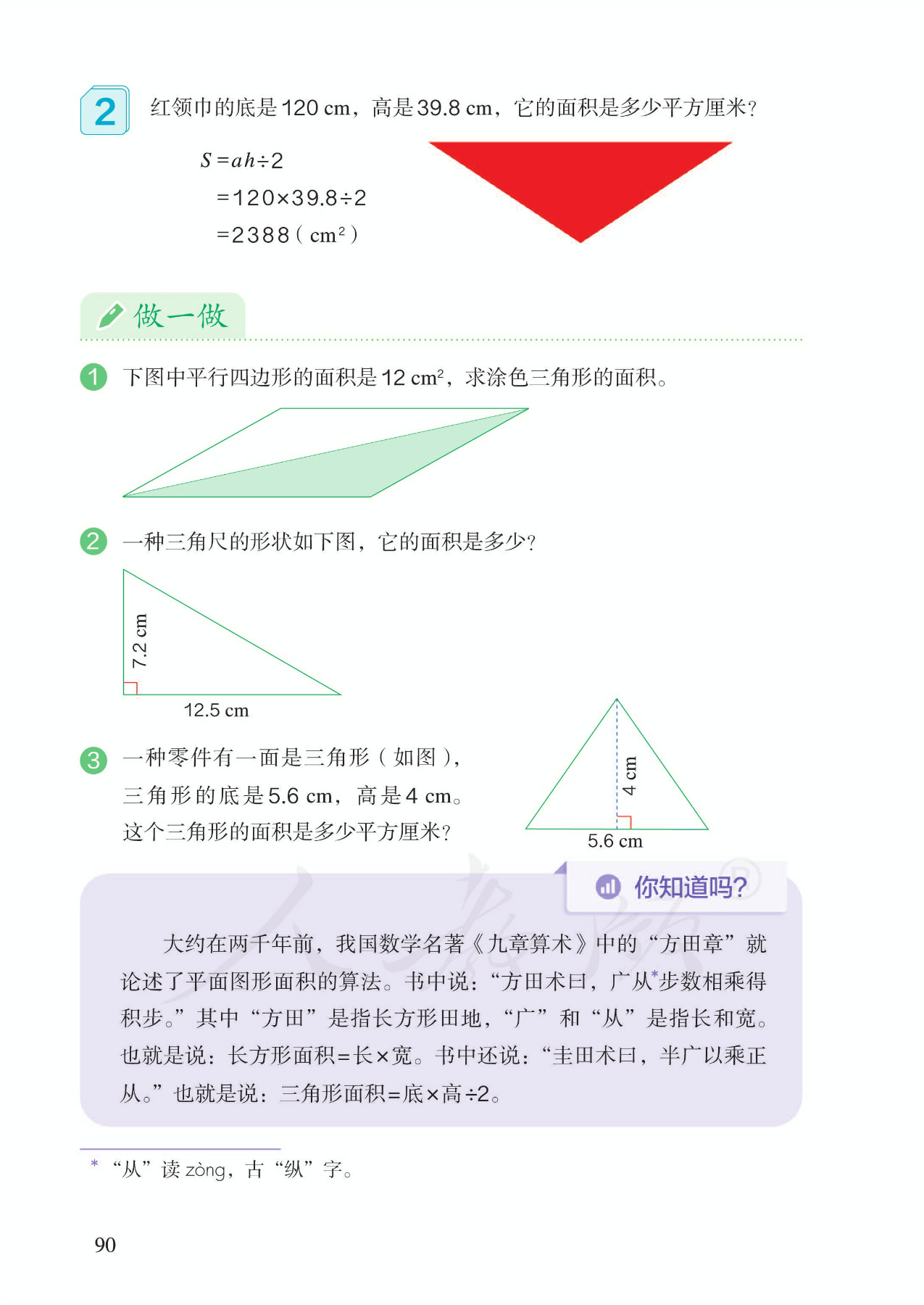



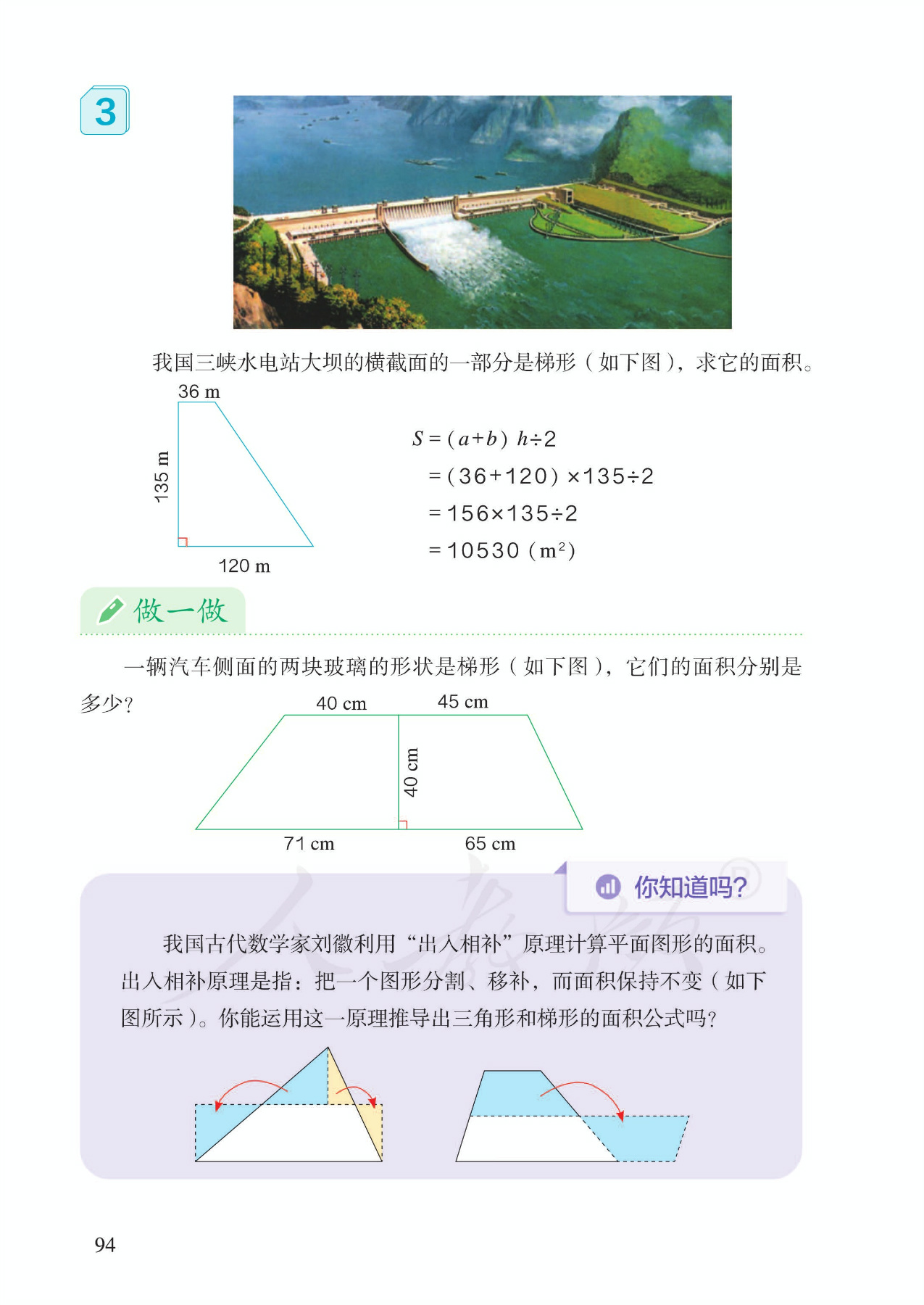
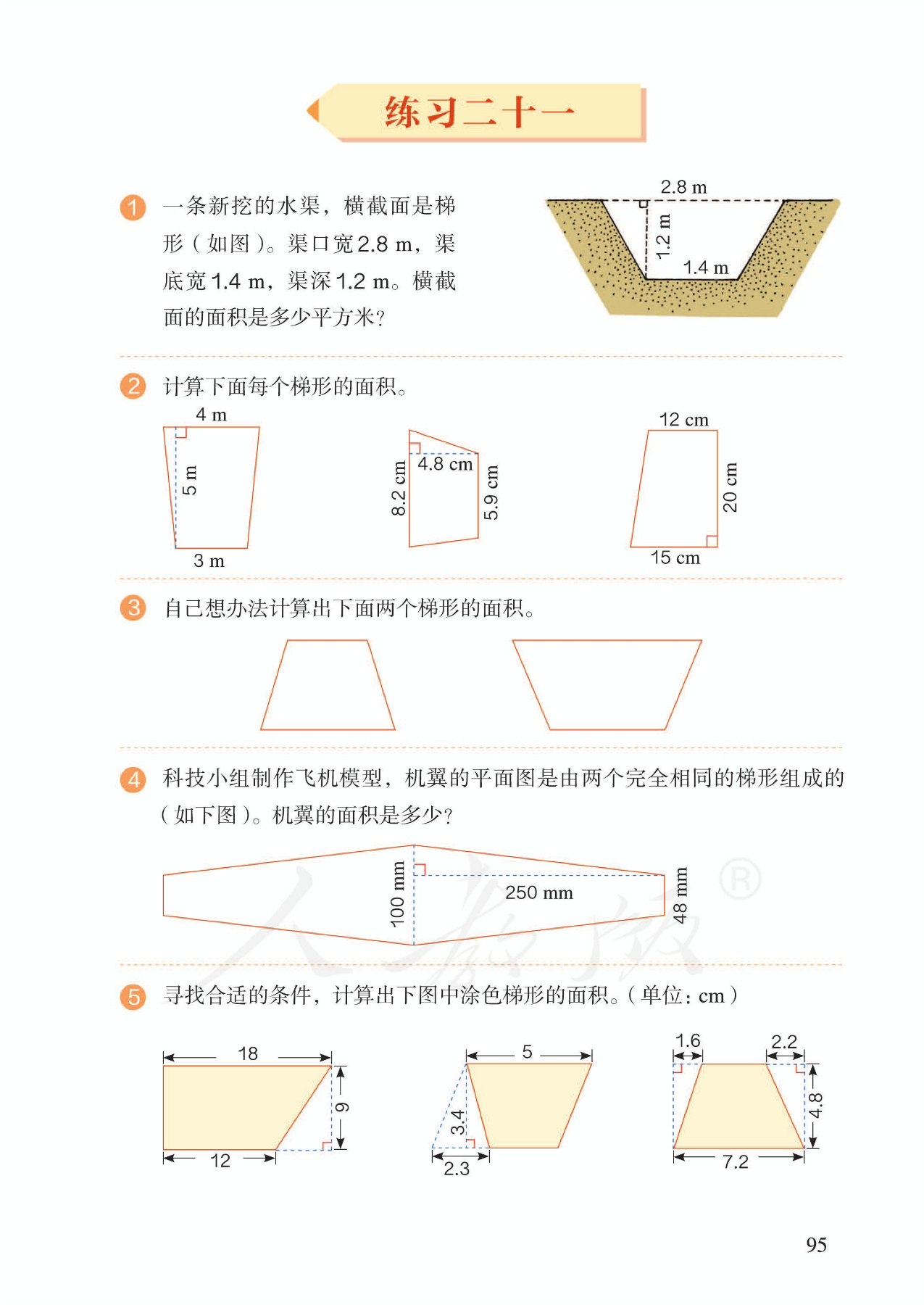

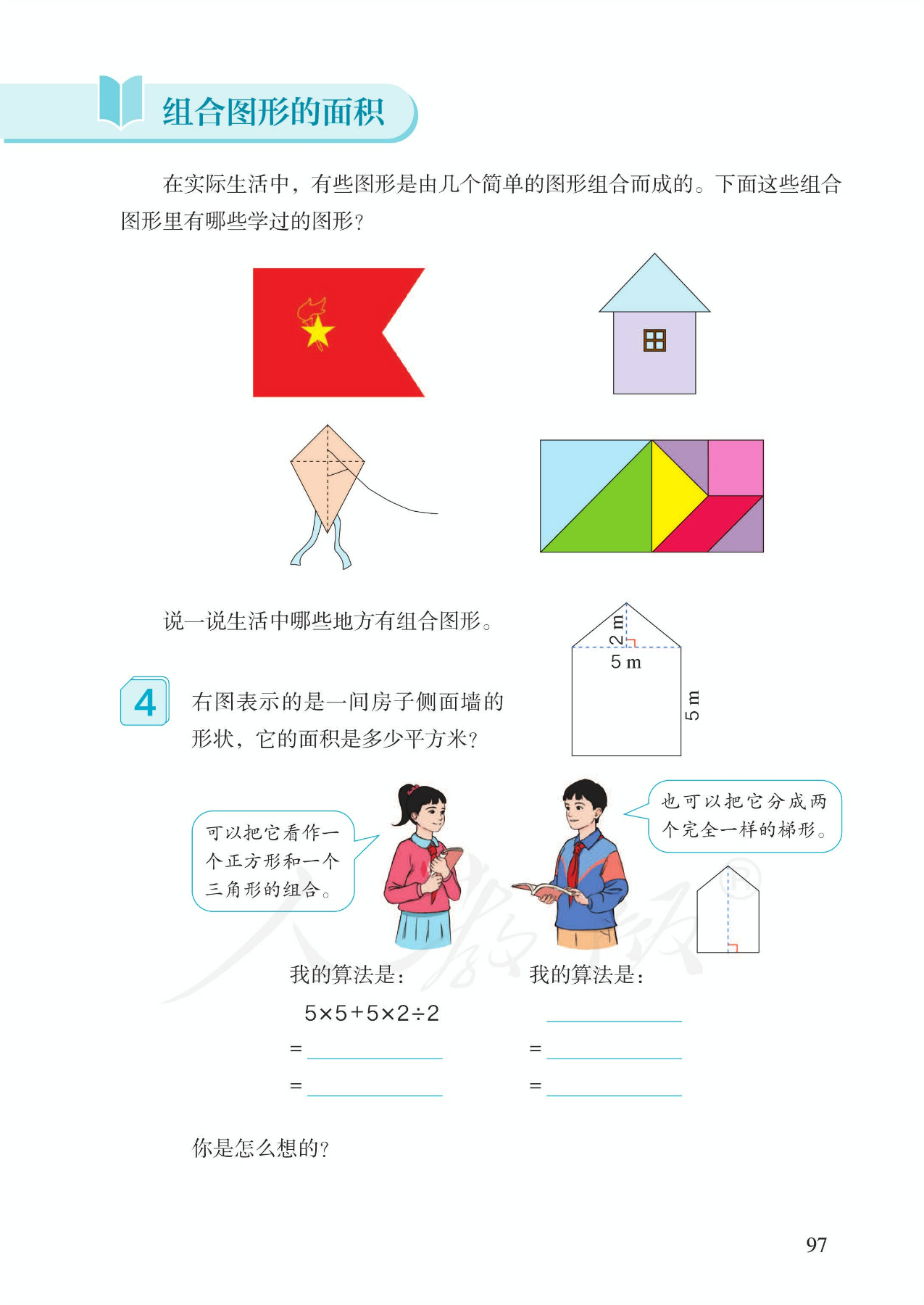

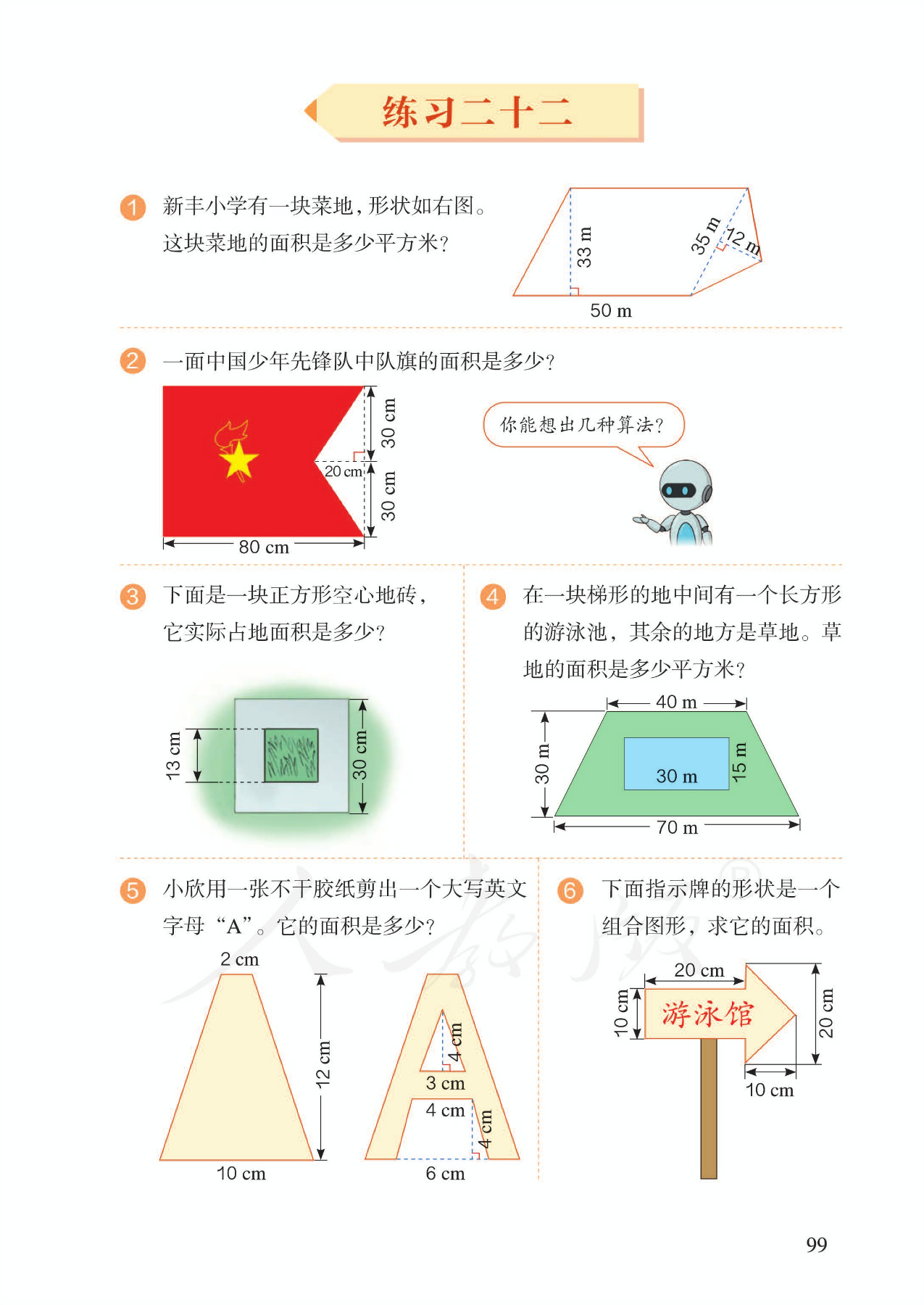


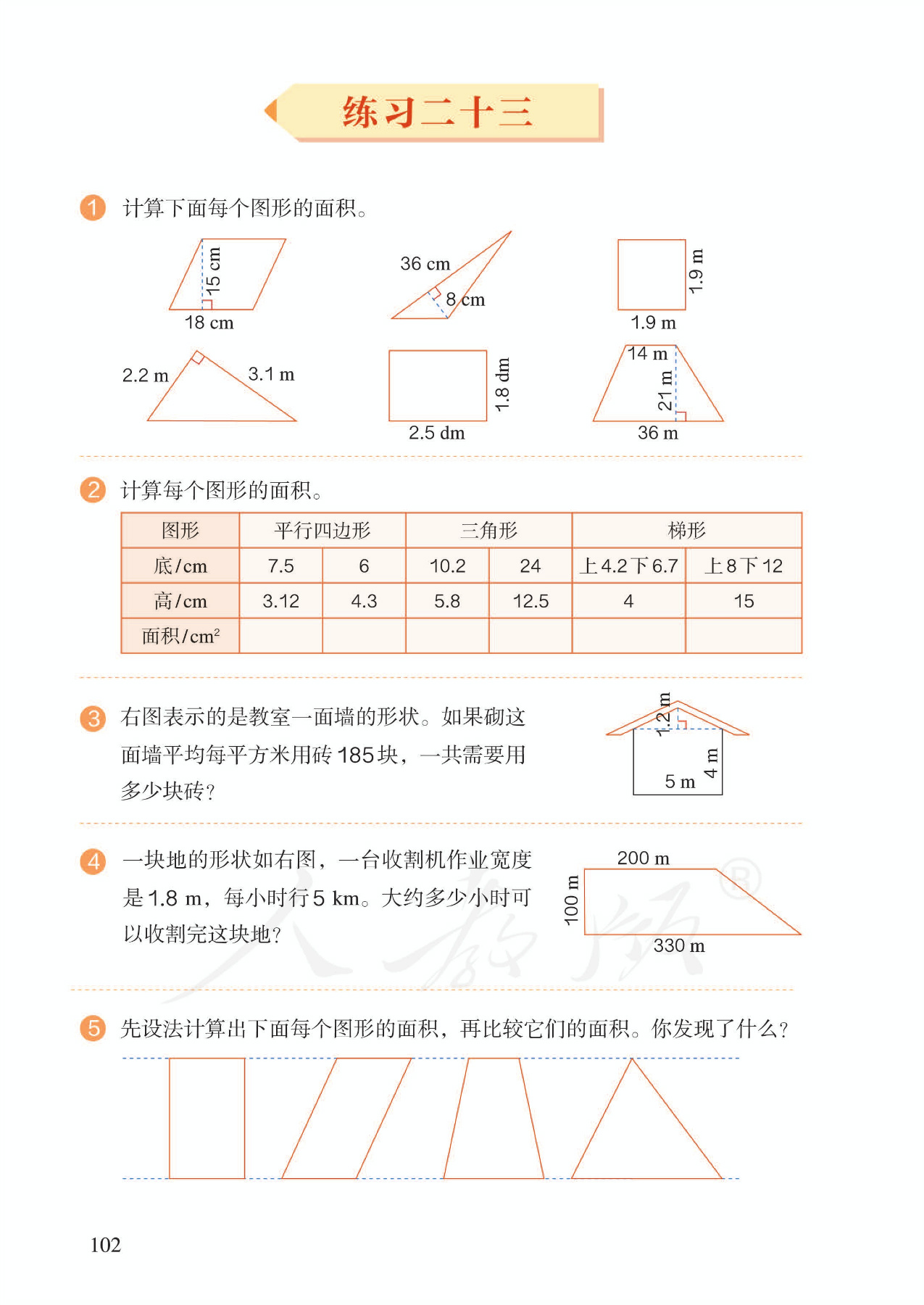

5 单元作业目标
1.能正确表示平行四边形面积、三角形面积、梯形面积计算公式的推导过程
2.能运用平行四边形面积、三角形面积、梯形面积的计算公式正确计算图形的面积
3.能灵活运用平行四边形面积、三角形面积和梯形面积的计算方法,解决具体情境中的问题
4.能把组合图形分解成已学过的平面图形,并正确计算它的面积
5.能将不规则图形转化为近似的平面图形,并利用方格纸(或给定的数据)合理估算它的面积
6 教材解读
本单元学习的内容主要包括:平行四边形、三角形、梯形和组合图形的面积及解决问题五个部分。通过这些内容的学习,一方面让学生运用转化的思想方法推导出平面图形的面积计算公式,积累数学活动经验;另一方面让学生在自主探索组合图形的面积等活动过程中发展空间观念。同时,也为进一步学习圆面积和立体图形表面积奠定基础。
教科书以长方形面积计算为基础,以图形内在联系为线索,以未知转化为已知的基本方法开展学习。注重突出学生自主探索的活动性,让学生动手实验,先将图形转化为已经学过的图形,再通过合作学习的方式,探索转化后的图形与原来图形的联系,从而发现新图形的面积计算公式。同时,按照学习活动的递进性,对学生探索的要求逐步提高,在学习知识的过程中培养学生动手操作、实验观察和分析推理的能力。
7 学情分析
学生在学习本单元之前,知道长方形、正方形、三角形的特征,会计算长方形、正方形的面积,对于“转化”的思想方法也有一定的认识,因此要求学生记住各种图形的面积计算公式并不难。但本单元面积计算公式的推导都是建立在学生数、剪、拼、摆的操作活动之上的,关键是要让学生经历探究的过程,实现过程性目标。
8 教学策略
1.重视动手操作与实践,让学生经历探索的全过程。本单元中多边形面积计算公式的推导都是建立在学生数、剪、拼、摆等操作活动中的。如平行四边形的面积计算中,“数方格”环节一定要让学生经历,因为 面积的多少就是一个个面积单位的积累 ,用“面积单位”铺是计算面积的基本方法,在数的基础上,引导学生发现平行四边形的底、高、面积与长方形的长、宽、面积之间的等量关系。在剪、拼、摆等操作活动中,利用几何直观,发展学生的空间观念,培养学生的空间想象能力。
2.注意渗透“转化”的数学思想方法。“转化”是数学学习和研究的一种重要思想方法,在这一单元的学习中发挥着积极的作用。一方面,在图形面积计算公式的推导中,都是将所研究的图形转化为已经会计算面积的图形;另一方面,组合图形的面积也是将其转化为基本图形来计算的。在教学中,要突出“将未知转化为已知”的基本转化思想,让学生通过操作,将所研究的图形转化为已经会计算面积的图形,探究所研究的图形与转化后的图形之间的联系,从而找到所求图形面积的计算方法。
9 单元目标
1.让学生通过动手操作、实验观察等方法,探索并掌握平行四边形、三角形和梯形的面积公式。
2.让学生会用面积公式计算平行四边形三角形和梯形的面积,并能解决生活中一些简单的实际问题。
3.让学生认识简单的组合图形,会把组合图形分解成已学过的平面图形并计算出它的面积。
4.让学生会用方格纸估计不规则图形的面积。
10 例题分析
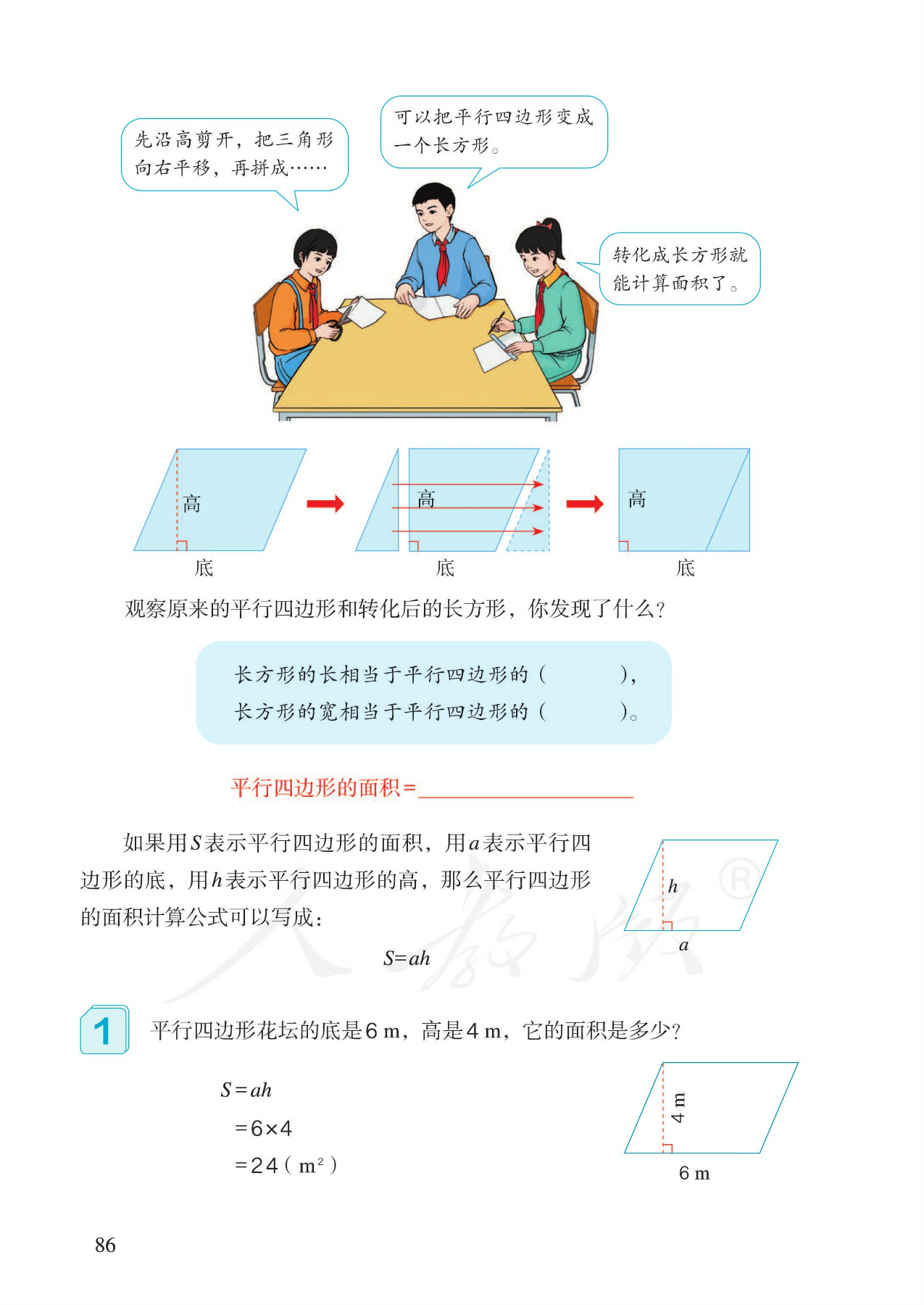
1.从主题图中的两个花坛(一个长方形,一个平行四边形)引出如何计算平行四边形面积的问题。先用数方格的方法试一试。探究平行四边形面积计算公式。突出转化思想。
2.继续渗透转化思想,帮助学生理解把未知转化为已知。转化以后,放手让学生自己观察,写出三角形的面积计算公式,特别要强调除以2的理解。最后用字母表示出面积计算公式。
3.转化的方式有多种:一种是分割的方法,把梯形剪成两个三角形,或将梯形剪成一个平行四边形和一个三角形;一种是拼摆的方法,用两个一样的梯形拼成一个平行四边形。教学时可以以拼摆方法为研究重点,让学生叙述推导的过程,得出梯形面积计算公式。
4.教学组合图形面积的计算,由于一个组合图形可以有不同的分解方法,也就有不同的面积计算方法。
5.借助方格纸估计不规则图形(树叶)的面积,这是估算思想在图形与几何中的应用。教学中,可以直接出示树叶,让学生思考怎样来估计它的面积,通过交流体会选择测量标准的重要性。并体会估算方法多样。
11 课时资料
| 课时名 | 年级单元 |
|---|---|
| 5a 多边形的面积复习课 |
喝咖啡记录:
| 日期 | 昵称 | 金额 | 备注 |
|---|---|---|---|
| 2024-04-09 21:42 | *颢 | ¥9.90 | 喝咖啡 |